What is a wave?. A wave is simply a disturbance that moves through a medium . Other waves do not require a medium to travel i.e. they can travel in a vacuum, are known as electromagnetic waves e.g. radio, X-rays, gamma rays UV rays etc. Other waves require a material medium to be transferred and are called mechanical waves i.e. water, sound waves etc.
Transverse and longitudinal pulses and waves.
- Transverse waves– they consist of a crest and a trough. In this case the displacement of the medium caused by these pulses are perpendicular to the direction in which the wave (disturbance) travels.
A pulse is a single non-repeated disturbance.
If the pulses are repeated periodically (regularly) they produce a series of waves called periodic transverse wave train.
They can be produced as shown below. Examples are water waves, light and radio waves.
- Longitudinal waves– these are waves whereby the particles of the medium vibrate parallel to the direction of movement of the disturbance .
When several turns of a spring are pulled together (compression) and then released they tend to spread out to their original position.
When pulled apart (rarefaction) they also turn to their original position.
In this case the displacement of the spring is parallel to the motion of the wave and this is known as longitudinal. Examples are the sound waves.
Characteristics of waves
- All waves have speed which depends on the nature of disturbance.
- All waves have wavelength (distance between two successive points in a wave ).
Represented by the symbol λ and is measured in metres. 3. All waves have frequency ‘f’ which is the number of waves passing a point in one second. It is measured in cycles per second or hertz (Hz). The period of a wave is the time required for a complete wave to pass a given point.
Therefore T = 1 / f or f = 1 / T (period is measured in seconds).
The speed ‘v’ is given as; v = λ / T, since f = 1 / T then v = (1 / T) × λ = f λ or v = f λ. This is the wave equation.
- All waves have amplitude which is the maximum displacement of the particles of the medium as the wave passes.
Examples
- A rope is displaced at a frequency of 3 Hz. If the distance between two successive crests of the wave train is 0.8 m, calculate the speed of the waves along the rope.
Solution
v = f λ = 3 × 0.8 = 2.4 m Hz = 2.4 m/s.
- The figure below illustrates part of the displacement-time graph of a wave travelling across water at a particular place with a velocity of 2 ms-1. Calculate the wave’s;
- a) Amplitude
- b) Frequency (f)
- c) Wavelength (λ)
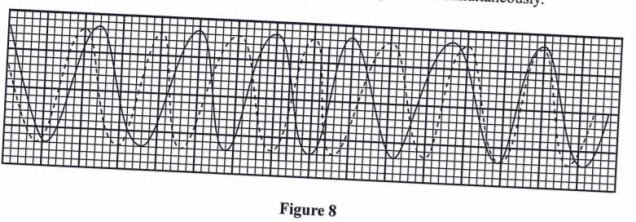
Solution
- a) From the graph, maximum displacement (a) = 0.4 cm
- b) From the graph, period T = time for one cycle = 0.20 seconds
So f = 1 / T = 1 / 0.20 = 5 Hz.
- c) Velocity = f λ hence λ = 2 / 5 = 0.4 m.
See also:
MAGNETIC EFFECT OF AN ELECTRIC CURRENT
EQUILIBRIUM AND CENTRE OF GRAVITY